La géolocalisation
Le système GPS (Global Positioning System) repose sur l’émission de signaux émis par un ensemble de 24 satellites situés sur une orbite à 20200 km d’altitude, signaux qui sont captés par notre récepteur GPS.
Chaque signal émis par un satellite donné contient des informations, notamment sa propre position et l’instant d’émission du signal. Le signal est émis vers la Terre, un peu comme un signal radio.

Prenons l’exemple de deux satellites, notés A et B, qui émettent chacun un signal à un instant donné. Comme illustré sur l’animation ci-dessous, au fur et à mesure que le temps s’écoule, les signaux se rapprochent de la Terre. Notre petit boîtier GPS reçoit d’abord le signal du satellite A, qui se trouve plus près de lui, puis celui du satellite B. Pour chaque satellite, il connaît ainsi l’instant d’émission du signal (information contenue dans le signal) et l’instant où il le reçoit, qu’il mesure lui-même. Autrement dit, il connaît la durée qui a été nécessaire pour parcourir chaque distance satellite-GPS. Le signal se déplace à la vitesse de la lumière, qui est parfaitement connue, donc le GPS peut calculer la distance qui le sépare de chaque satellite. Il sait également où se trouve chaque satellite dans l’espace. Ce qui lui reste donc à connaître, c’est où il se trouve lui, dans l’espace.
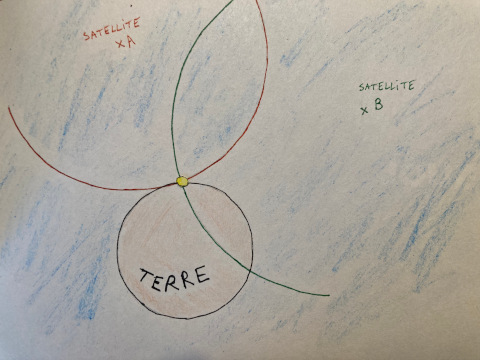
Pour cela, il fait un calcul qui peut être schématisé par le dessin suivant. Le GPS se situe à l’intersection des cercles ayant pour centres les positions des satellites, et pour rayons les distances satellite-GPS. Il y a deux intersections possible, mais le GPS sait qu’il se trouve sur la surface de la Terre, donc qu’il se situe au point représenté par la pastille jaune. C’est le principe de la géolocalisation.
En réalité, l’espace est en trois dimensions (alors que le dessin est en deux dimensions), donc il faut trois satellites et non deux pour réaliser cette localisation. On utilise même en général un quatrième satellite pour plus de précision.
GPS et relativité du temps
Le fonctionnement du GPS se trouve être une des applications les plus usuelles de la théorie de la relativité d’Einstein. En effet, une difficulté se cache dans tout le principe de géolocalisation qui vient d’être détaillé. Le calcul de la durée de déplacement du signal est calculé à partir de deux informations :
- L’instant où le signal est émis, mesuré par l’horloge du satellite.
- L’instant où le signal est reçu, mesuré par l’horloge du GPS.
Or… le temps ne s’écoule pas à la même vitesse pour le satellite et pour le GPS ! Si bien que ces deux horloges… ne sont pas synchronisées. Comment ce problème est-il pris en compte et résolu, c’est ce que nous allons voir, après avoir présenté la théorie de la relativité.
Qu’est-ce que c’est la théorie de la relativité ?
La relativité d’un mouvement peut être appréhendée dans la perception quotidienne lors du déplacement d’un objet par rapport à un autre. Lorsque nous marchons sur un tapis roulant, nous comprenons facilement que notre vitesse n’est pas la même dans le référentiel du tapis roulant, et dans le référentiel du sol fixe. C’est tout l’intérêt du tapis roulant d’ailleurs : notre vitesse de marche et la vitesse du tapis roulant s’ajoutent et on arrive plus vite au bout. Nous pouvons ainsi formuler la vitesse d’un objet dans deux référentiels différents R1 et R2. Si ces référentiels sont inertiels, c’est-à-dire qu’ils se déplacent à vitesse constante l’un par rapport à l’autre, alors la vitesse d’un l’objet dans le référentiel R2 est égale à la vitesse du même objet dans le référentiel R1, additionnée de la vitesse du référentiel R2 dans le référentiel R1.
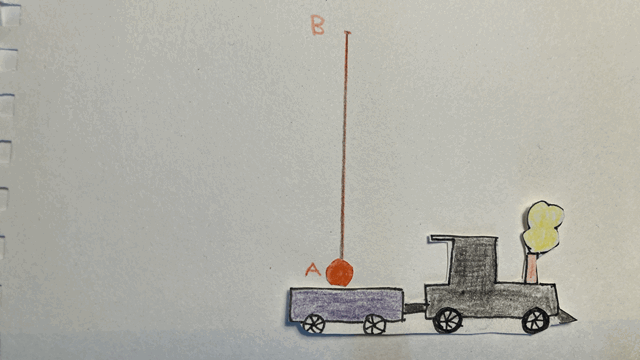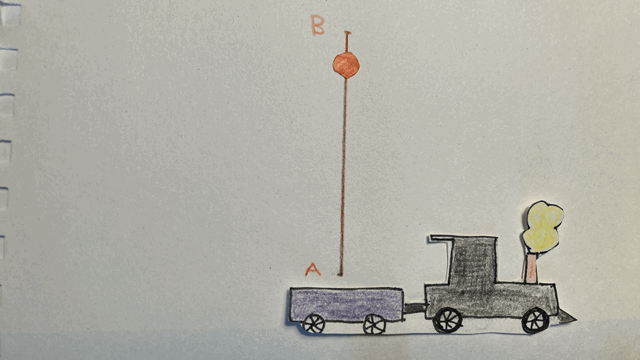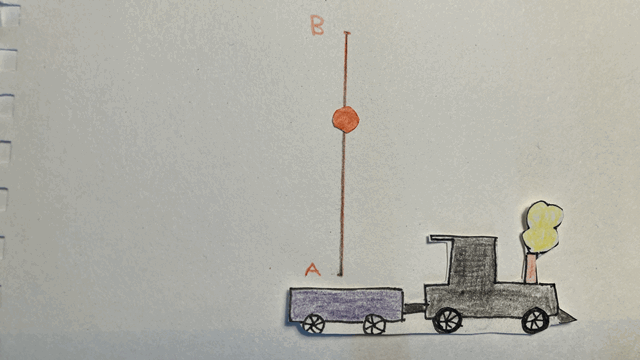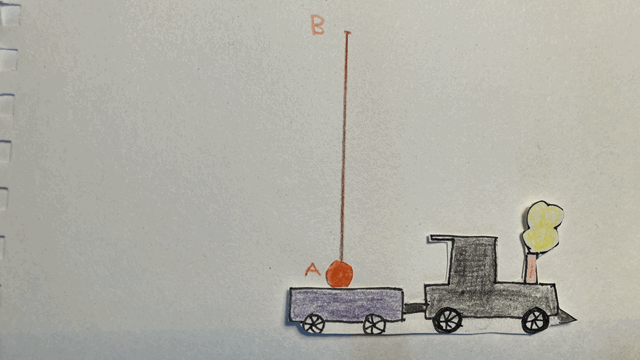
Allons un peu plus loin dans l’étude des référentiels. Le premier « postulat » que nous utiliserons spécifie que « les lois de la physique sont les mêmes pour tous les observateurs se trouvant dans des référentiels inertiels ». En particulier, si je lance une balle vers le haut, peu importe que ce soit sur la terre ferme ou dans un train qui se déplace, cette balle aura une trajectoire verticale. Imaginons donc que je sois dans un train, et que je lance ma balle vers le haut. De mon point de vue, aucune surprise, elle monte et redescend, en parcourant la trajectoire A-B-A. Ainsi, durant la durée définie par son départ et son retour au point A, la balle a parcouru une distance totale égale à deux fois le segment AB dans le référentiel du train.
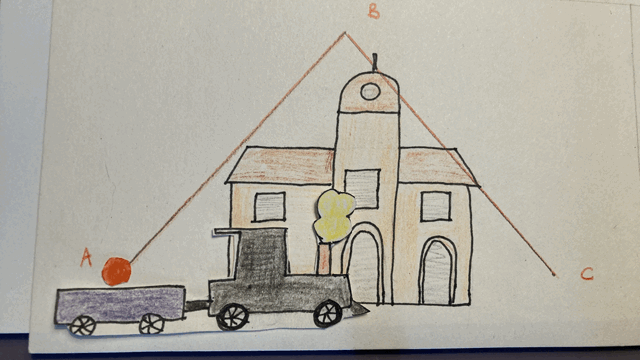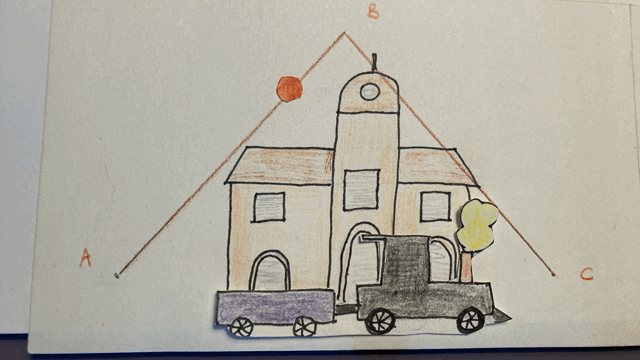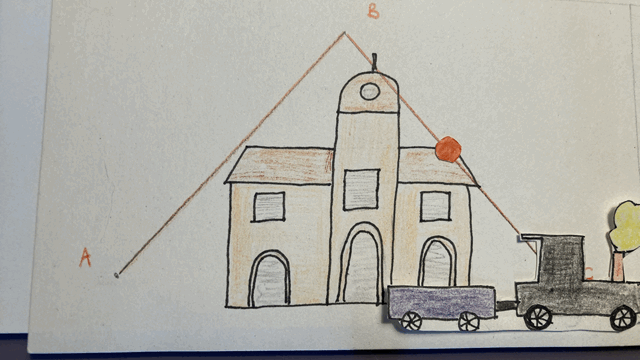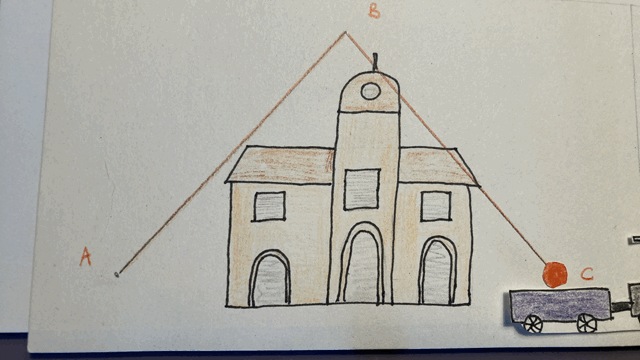
Mais imaginons qu’un observateur observe la scène depuis la gare. Il voit à la fois le mouvement de la balle par rapport au train et le mouvement du train par rapport à la gare. De son point de vue, autrement dit dans le référentiel de la gare, la balle parcourt la trajectoire A-B-C, dont la distance est égale à la somme des segments AB et BC. Nous observons que dans le référentiel de la gare, la balle parcourt une distance plus grande que dans le référentiel du train, dans la même durée de temps. Cela n’a rien d’étonnant, puisque la vitesse de la balle est plus grande dans le référentiel de la gare que dans celui du train (vitesse de la balle par rapport au train + vitesse du train par rapport à la gare).
Le second « postulat » que nous utilisons à présent, spécifie que « la vitesse de la lumière dans le vide a la même valeur dans toutes les directions et dans tous les référentiels inertiels ». Notons que ce postulat, comme le précédent, a fait l’objet de nombreuses vérifications expérimentales, qui n’ont jamais montré d’exception. Précisément, la lumière parcourt 299 792 458 mètres par seconde dans le vide.
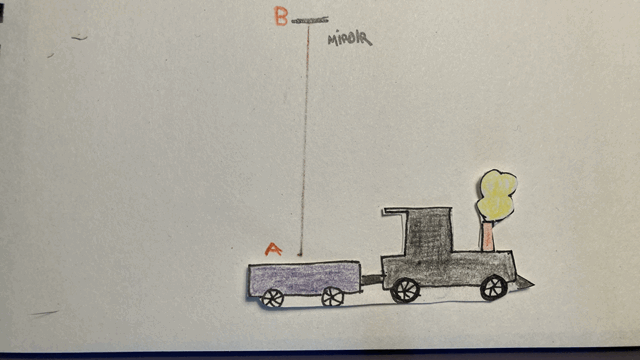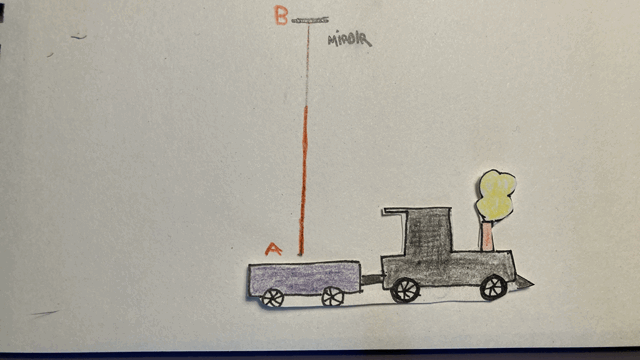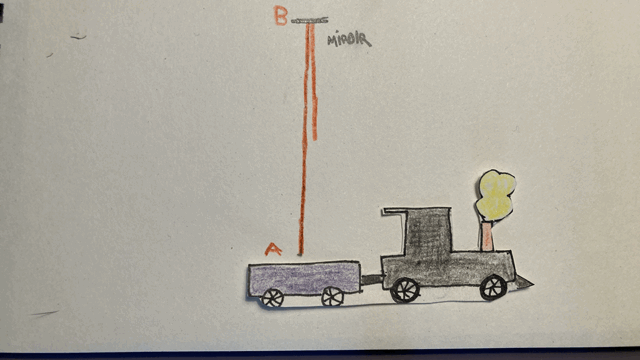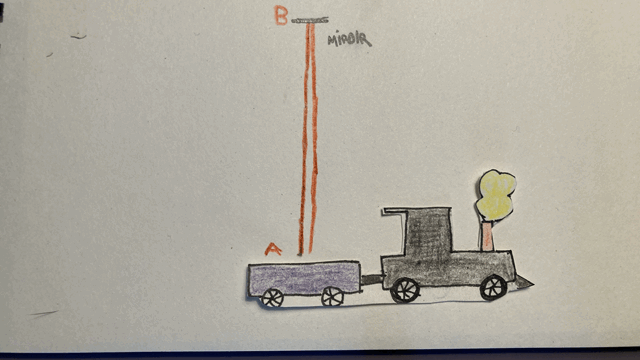
Imaginons alors une expérience semblable à la précédente, où cette fois il ne s’agit pas d’une balle mais d’un rayon lumineux que je fais partir à la verticale, alors que je me trouve dans le train. Cela pourrait être un rayon laser rouge qui se réfléchit sur un miroir placé au-dessus de moi. Exactement comme dans le cas précédent, le rayon lumineux parcourt la distance AB-BA dans le référentiel du train, et la distance AB-BC dans le référentiel de la gare. Mais cette fois, le second postulat affirme que la vitesse de ce rayon lumineux est la même dans les deux référentiels (contrairement à la balle). Autrement dit, la vitesse de la lumière et la vitesse du train ne s’additionnent pas.

Cela semble un casse-tête : le rayon, avec la même vitesse, parcourt dans un cas une distance plus grande que dans l’autre, et ce dans le même laps de temps… Ce casse-tête se résout si l’on considère la chose suivante : la durée de temps écoulée entre le départ du rayon et son retour au point initial n’est pas la même dans les deux référentiels. Le temps s’est écoulé plus vite dans le référentiel du train.
Autrement dit, le temps ne s’écoule pas de la même manière dans tous les référentiels, ce qui découle directement de cette propriété très particulière de la vitesse de la lumière définie par le second postulat.
Désormais, on ne peut plus considérer un temps qui s’écoule de la même manière partout, indépendamment de l’espace dans lequel les objets se déplacent. Temps, vitesse et espace sont intimement reliés et on parle d’un ensemble espace-temps. Le temps peut ainsi se dilater ou se contracter selon le référentiel où l’on se place, et il en est de même de l’espace. Ce phénomène peut sembler surprenant, contre-intuitif et sorti du cerveau d’un savant fou. Mais il a été mesuré et vérifié dans un très grand nombre de situations depuis sa description par Einstein en 1905, sans jamais être mis en défaut.
Pour en revenir à la géolocalisation, qui nous intéresse ici, nous comprenons à présent que le satellite se déplaçant à une certaine vitesse par rapport à la Terre, le temps s’y écoule plus vite que sur Terre, comme c’est le cas dans le train. Ainsi les horloges qui se trouvent sur Terre et celles qui se trouvent dans les satellites ne sont pas synchronisées. Quelle erreur cela représente t’il et à quel point cela pose t’il problème pour se localiser ? Nous allons y venir, avec quelques calculs.
Mais pour l’instant, nous allons nous attaquer à la relativité générale.
De la relativité restreinte à la relativité générale
Jusqu’ici, nous avons décrit les effets dus à ce que l’on appelle la « relativité restreinte », qui ne concerne que les référentiels inertiels (donc se déplaçant à vitesse constante les uns par rapport aux autres). Faisons un pas de plus vers la relativité générale, qui s’applique aux situations où des objets ne se déplacent plus à vitesse constante, mais où ils accélèrent ou bien ralentissent, soumis à des forces extérieures. Le modèle de la relativité générale a également été développée par Einstein, et il l’a publié en 1915.
Une situation courante est celle d’un objet qui tombe vers le sol. Pourquoi tombe-t-il ? Parce qu’il est soumis à la gravité, à l’attraction terrestre. On peut utiliser un autre terme et dire qu’il est soumis un champ gravitationnel, orienté vers le centre de la Terre. Lorsqu’un objet est en chute libre, il accélère au fur et à mesure du temps. Sa vitesse n’est pas constante, et il ne représente pas un référentiel inertiel par rapport à la Terre. Par ailleurs, deux objets, quelles que soient leurs poids, lâchés au même instant et au même endroit, tous deux soumis au même champ gravitationnel, ont exactement le même mouvement, ils restent immobiles l’un par rapport à l’autre. Ceci à condition qu’ils n’y ait pas d’autre force, comme les frottements de l’air, qui les ralentisse. Ainsi, si vous lâchez un kilo de plomb et une plume, dans le vide, ils tomberont ensemble. En revanche, dans l’atmosphère terrestre, la plume chutera moins vite, ralentie par les frottements de l’air.

Imaginons alors la situation représentée par deux balles, une rouge et une verte, se trouvent dans un ascenseur vitré situé dans l’espace. Cette expérience aurait pu être menée par Willy Wonka, Charlie et son grand père dans « Charlie et le grand ascenseur de verre », de Roald Dahl, paru en 1972.
Nous voyons deux balles flottant immobiles l’une par rapport à l’autre dans l’ascenseur. Cet ascenseur pourrait donc bien être en chute libre vers la Terre. Cependant, un autre scénario est possible : l’ascenseur pourrait tout aussi bien se trouver à distance tellement grande de la Terre et de tout autre astre, qu’il ne subirait aucune gravité, il serait alors en apesanteur. Impossible de savoir. Vu de l’ascenseur, ces deux scénarios : chute libre et apesanteur sont parfaitement équivalents.
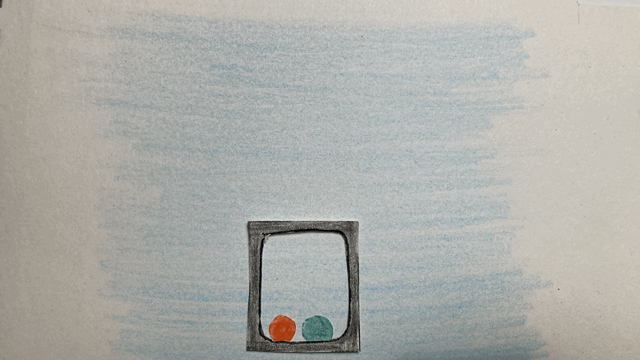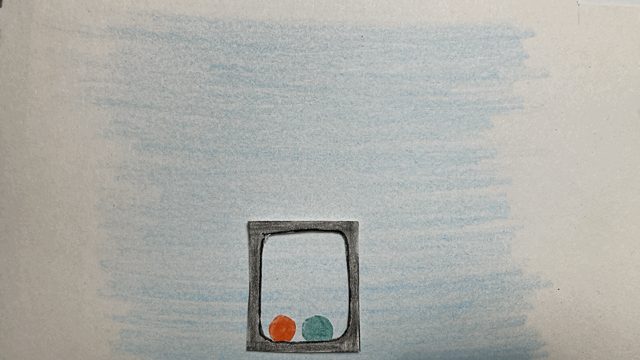
Autre situation représentée sur cette figure-ci : deux balles sont plaquées au sol de l’ascenseur. Que se passe-t-il cette fois ? L’ascenseur pourrait être immobile sur la Terre, situation assez courante. La force de gravité s’applique sur les balles, si bien qu’elles restent sur le sol de l’ascenseur. Mais là aussi, un autre scénario est possible : l’ascenseur pourrait se trouver loin de la Terre, mais soumis à une accélération vers le haut (comme celle que subissent les astronautes au décollage de leur fusée), qui les plaquerait au sol. De nouveau, il est impossible de savoir pour un observateur à l’intérieur de l’ascenseur. Les deux scénarios, ascenseur immobile dans un champ gravitationnel orienté vers le bas, et ascenseur accéléré vers le haut, sont parfaitement équivalents.
Cette impossibilité à discriminer entre deux scénarios, on l’appelle le principe d’équivalence.
- Il est parfaitement équivalent d’être en chute libre ou d’être en apesanteur.
- Il est parfaitement équivalent d’être immobile dans un champ de pesanteur orienté vers le bas ou d’être accéléré vers le haut.

Pour continuer, nous allons nous placer dans un ascenseur vitré, accéléré vers le haut dans l’espace intersidéral (donc loin de tout étoile ou planète). Par ailleurs, un rayon laser, émis depuis l’espace, se déplace tout droit et traverse l’ascenseur. Vu de l’extérieur de l’ascenseur, nous voyons l’ascenseur monter au fur et à mesure que le faisceau le traverse.

En revanche, vu depuis l’intérieur de l’ascenseur, nous voyons le faisceau lumineux aller vers le bas. Comme l’ascenseur accélère en montant, sa trajectoire semble avoir cette forme de cloche.
Tout cela est très intéressant, me direz-vous, mais où voulons nous en venir ? Et bien selon le principe d’équivalence, ce que je viens de décrire dans un ascenseur soumis à une accélération vers le haut, doit également s’appliquer dans un ascenseur immobile dans un champ de pesanteur. Autrement dit, le rayon lumineux doit également être incurvé dans un champ de pesanteur. Et c’est bien ce qui se passe.
En effet la lumière est déviée sous l’effet d’un champ gravitationnel. Par exemple, un rayon lumineux passant près de la Terre, (ou d’une autre planète, ou d’une étoile) s’incurve sous l’effet de son champ gravitationnel. À notre échelle habituelle, ce type de phénomène est invisible. Mais les astrophysiciens l’observent tous les jours lorsqu’ils pointent leurs télescopes vers le ciel.
Ce phénomène a également une conséquence sur l’écoulement du temps à l’intérieur et à l’extérieur de l’ascenseur. Dans le référentiel de l’espace, la distance parcourue par le faisceau lumineux entre l’instant où le faisceau pénètre dans l’ascenseur et l’instant où il en sort est un segment égal à la largeur de l’ascenseur. En revanche, dans le référentiel de l’ascenseur, la distance parcourue entre les mêmes instants est la courbe en forme de cloche, qui est plus longue que le segment. Or, vous le savez maintenant, la vitesse de la lumière est la même dans tous les référentiels. La seule solution possible pour expliquer que le rayon lumineux parcourt un trajet plus long dans l’ascenseur est donc que le temps s’écoule moins vite dans l’ascenseur.
Plus généralement : le temps s’écoule plus lentement dans un référentiel soumis à un champ gravitationnel, d’autant plus que ce champ est fort. Le film Interstellar, sorti en 2014, en donne une illustration : le héros, parti dans l’espace à la recherche d’une planète vivable, s’approche d’un trou noir, extrêmement massif, donc générant un champ gravitationnel énorme. Le temps s’y écoule tellement lentement qu’une fois rentré sur Terre, il retrouve sa fille… désormais plus âgée que lui. Certes c’est un film et aucun humain n’a vécu pareille aventure, mais en principe, c’est en effet ce qui arriverait.
Revenons nous aussi sur Terre, et voyons comment ce problème de temps qui s’écoule plus ou moins vite concerne la géolocalisation par GPS. Le satellite se trouve plus loin du centre de la Terre que le GPS. Aussi, il subit un champ gravitationnel plus faible que le GPS (plus on s’éloigne de la Terre, plus l’attraction terrestre diminue). Donc, le temps s’écoule moins vite dans le satellite que sur Terre.
Où l’on estime l’effet de la relativité sur la géolocalisation
Nous avons qualitativement décrit deux effets :
- le satellite se déplace par rapport à la Terre avec une certaine vitesse, donc le temps s’y écoule plus vite qu’à la surface de celle-ci,
- le satellite, loin de la Terre, subit une gravitation moindre, donc le temps s’y écoule plus lentement qu’à sa surface.
Les deux effets vont en sens inverses, il nous faut donc en venir aux calculs pour estimer l’effet global : quelle est la différence d’écoulement du temps entre la Terre et le satellite ? Vous pouvez regarder le détail des calculs sur l’image ci-dessous… ou vous contenter du résultat.
- l’écart dû à la vitesse du satellite se calcule à partir de cette vitesse et de la vitesse de la lumière. Sur une période de 24 heures, le temps dans le satellite est plus court d’une durée de 7 microsecondes [1].
- l’écart dû à la différence de champ gravitationnel se calcule à partir du rayon de l’orbite du satellite, du rayon de la Terre, de la constante gravitationnelle et de la masse de la Terre. Sur une période de 24 heures, le temps dans le satellite est plus long d’une durée de 45 microsecondes.
En tenant compte des deux phénomènes, sur une période de 24h, le temps dans le satellite est plus long que le temps du GPS avec un écart de 38 microsecondes.
Bien… et donc ? On l’a dit, le boîtier GPS transforme les durées en distance. L’écart en distance se calcule en multipliant l’écart en durée par la vitesse de la lumière… et vaut plus de 11 km.
Ainsi, ne pas prendre en compte l’écart de durée dû aux effets relativistes aboutirait au bout de 24h à une erreur de positionnement de 11 km…
Pour éviter cette dérive, les horloges qui équipent les satellites du système GPS sont synchronisées avec les horloges terrestres par un réglage qui compense cette différence. Et la localisation GPS offre une précision de l’ordre du mètre. Lorsque nous utilisons un GPS, nous pratiquons ainsi la théorie de la relativité sans le savoir… Enfin, désormais, si, nous le savons.
Quelques précisions supplémentaires avant de refermer cette page
Les effets relativistes ne sont pas les seules sources d’erreur pour la localisation par GPS. En particulier, la vitesse de la lumière, qui joue un rôle majeur dans les calculs est parfaitement connue dans le vide, mais elle varie en fonction du milieu dans lequel les signaux se propagent. Entre le satellite et la Terre, les signaux traversent d’abord le vide, puis l’atmosphère terrestre, dont la composition varie avec l’altitude. L’effet de l’atmosphère sur la vitesse de la lumière dépend de la pression, de la température, de l’humidité, de la présence de nuages… Ces effets sont pris en compte du mieux possible dans la synchronisation des horloges.
Dans les faits, la précision est nettement améliorée par l’utilisation de quatre satellites au lieu des trois a priori nécessaires pour la géolocalisation, ce qui permet, à l’aide de calculs bien effectués, de s’affranchir en partie de ces erreurs.
Enfin, le GPS étant d’origine militaire, son utilisation civile est en mode volontairement dégradé et le détail des corrections d’horloge apportées est couvert par le secret défense.


